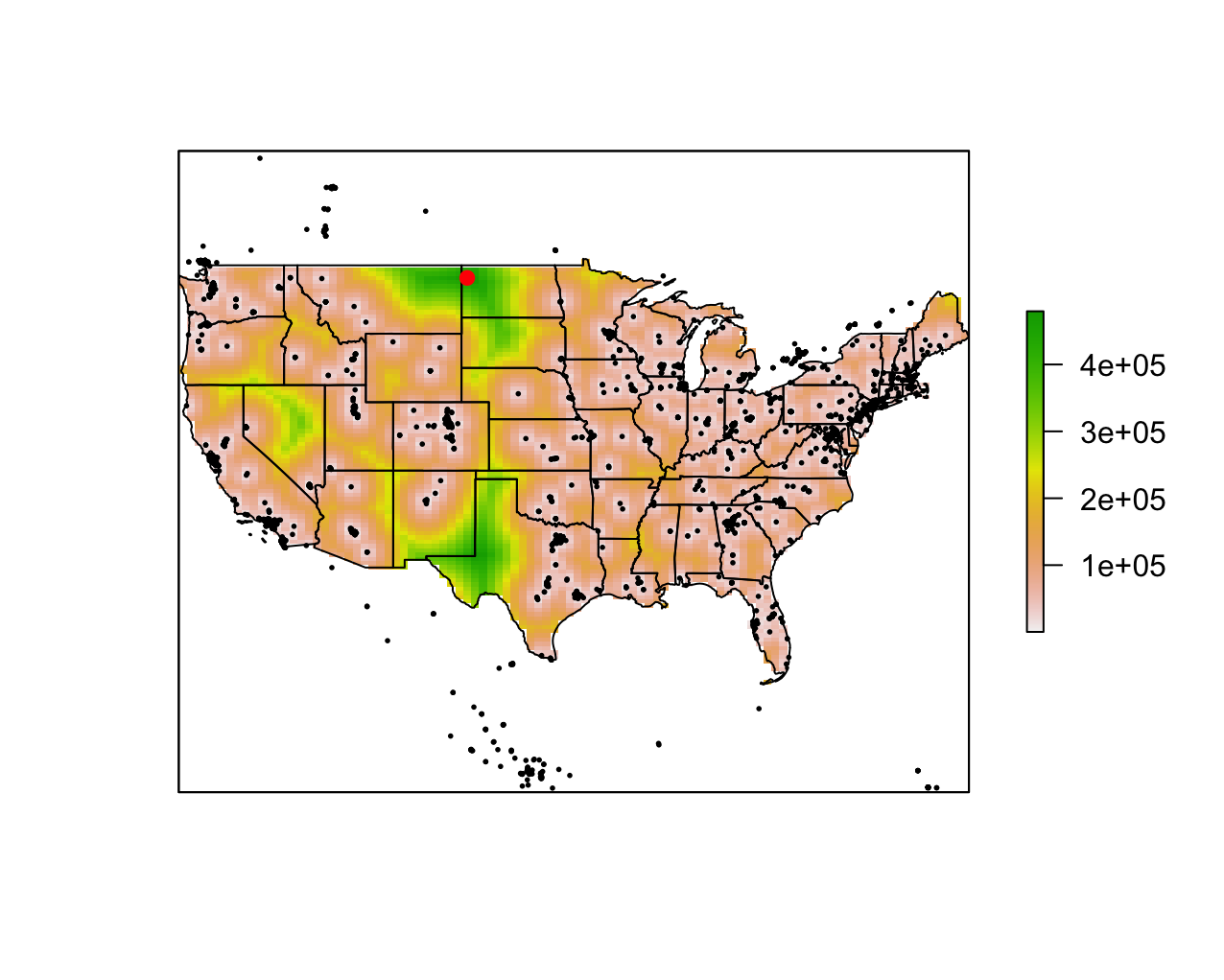
Raster map representing distance from nearest WCA competition (USA)

Interactive normal distribution PDF plot

McGill Diversity in Math logo (roughly) remade in Mathematica

Henon map in MatLab (single initial condition) $$x_{n+1}=1-a{x}_n^2+y_n$$ $$y_{n+1}=b{x}_n$$